Marathon Match 150 QueenAttack Postmortem
Problem
Last submission
MM150 last submission · GitHub
Strategy
The following process is repeated at high speed and the one with the best score is adopted.
- By using SA method to obtain an arrangement in which the queens do not collision with each other as much as possible.
- Assign queen locations using min-cost flow for the obtained placement
- Move to the assigned placement using the Dijkstra method.
Obtain an arrangement
The first step is to search for a queen arrangement by SA. A neighboring state is as follows
- Choose the highest number of collisions with other queens among some queens and move to the place with the lowest number of collisions with other queens among some empty spaces.
After the operation, the score is evaluated to determine whether the new state is adopted. This process is repeated until the time limit is exceeded or there are no more collisions between queens (Errors == 0).
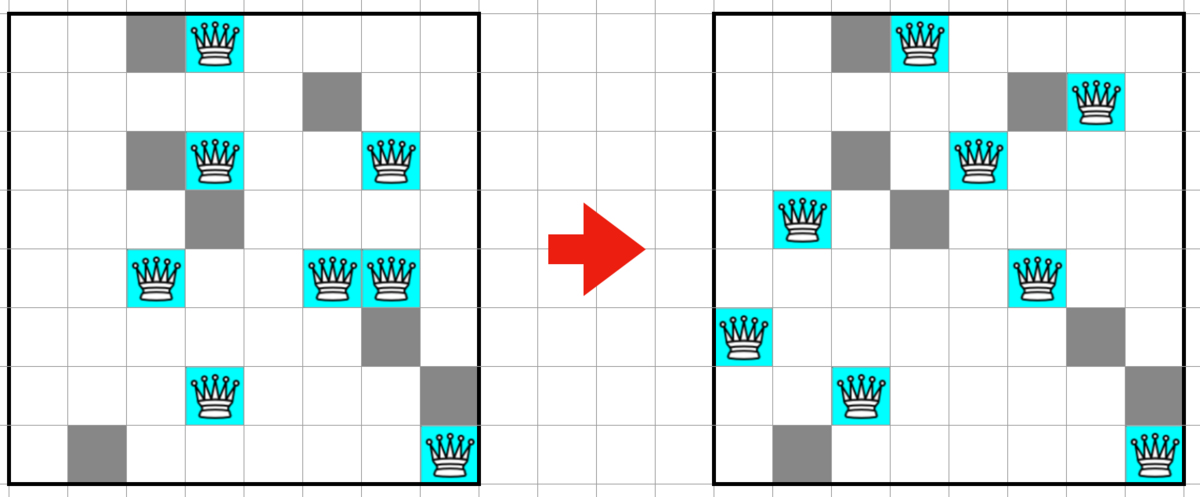
Faster collision detection.
To speed up the determination of whether queens are in collision with each other, the range of influence of queens is counted and its value is checked to speed up the collision determination.
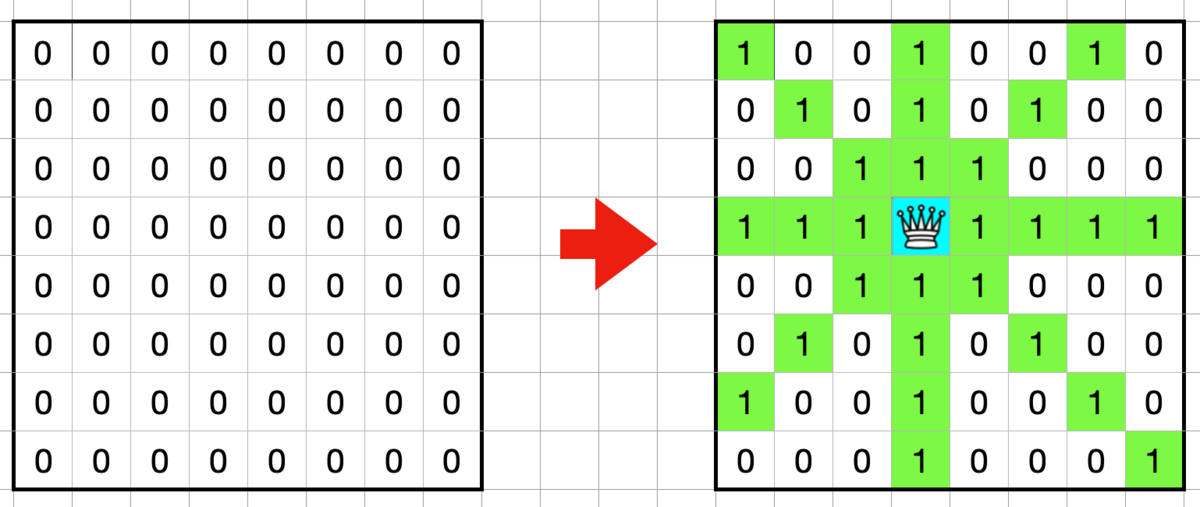
This information has for each color, and the number of values written indicates the number of collisions with other queens.
Assign position
For the arrangement obtained, which queens move to which position is determined using the min cost flow. As a cost, the raw score is used as the basis for the extra costs incurred when passing queens.
Move it to the assigned position
Once the allocation is complete, move the queen to that position using the Dijkstra method. Treat other queens as immobile when moving. The queens that can be moved to the destination are moved with the lowest cost and the process is repeated until there are no more queens left to move.
Randomly change the order in which they are moved.
If the queens are moved in order of decreasing cost, the order of the queens to be moved is fixed, but by adding a random value to the cost, the order of movement is not fixed. This process of moving the queens is executed several times and the one with the lowest cost is adopted.
Summary
When I saw it as a problem, I thought that bowwow's solution of AHC013 might work, but it looked like it would be troublesome to implement, so I went through with it and implemented it as it was using the strategy I thought of. The N-queen problem itself could be solved fairly fast, but in the end I couldn't manage the extra diversions and extra cost if I made the operation based on the assumption that I didn't move other queens when I moved them.