問題
A - Recurring Cleaning Route
戦略
ビームサーチパートは 500msec (テストケースによってはもっと速く終わる)、焼きなましパートは 1500msec 使用しています。
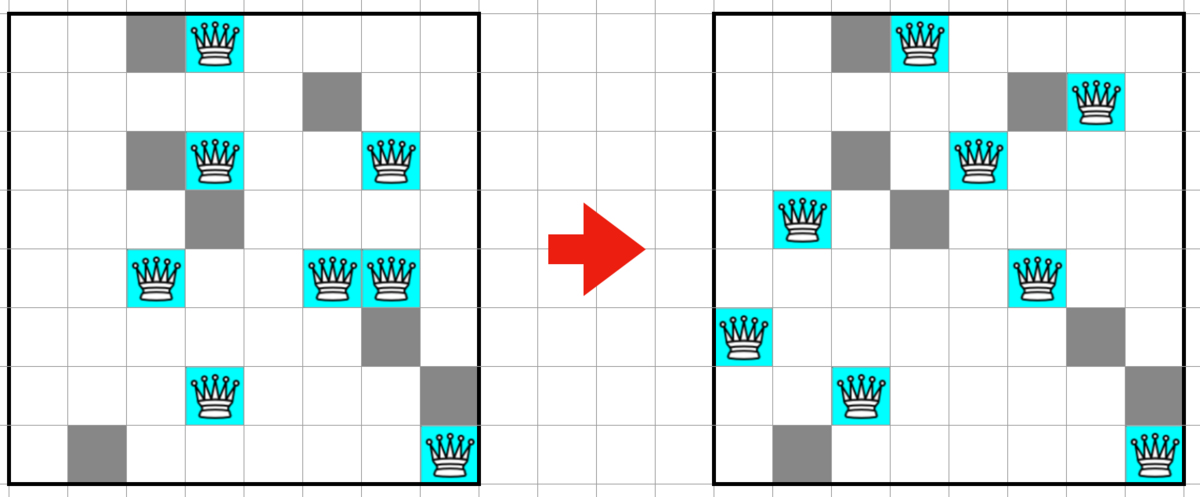
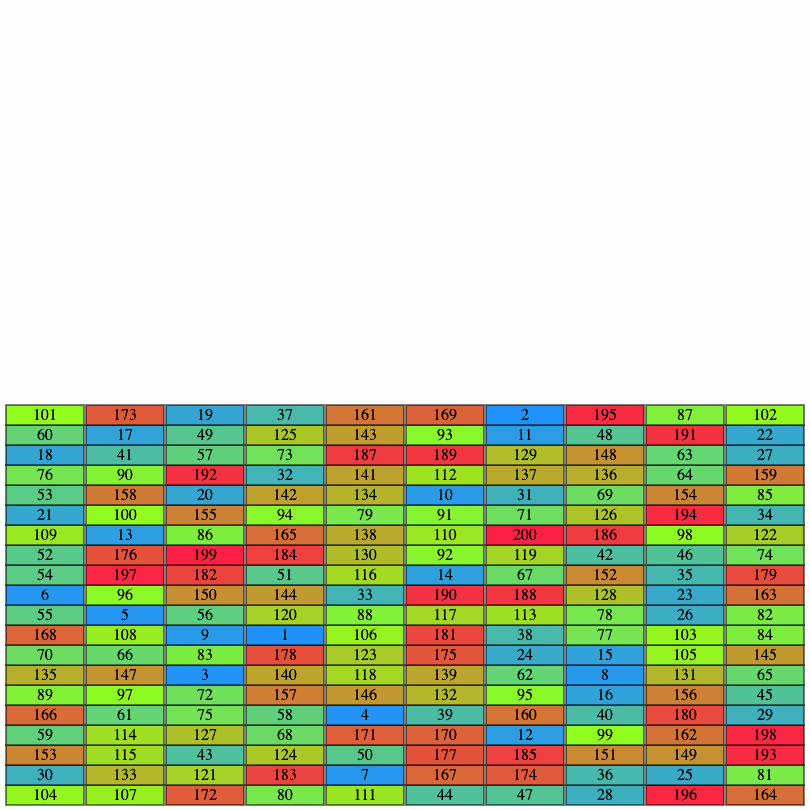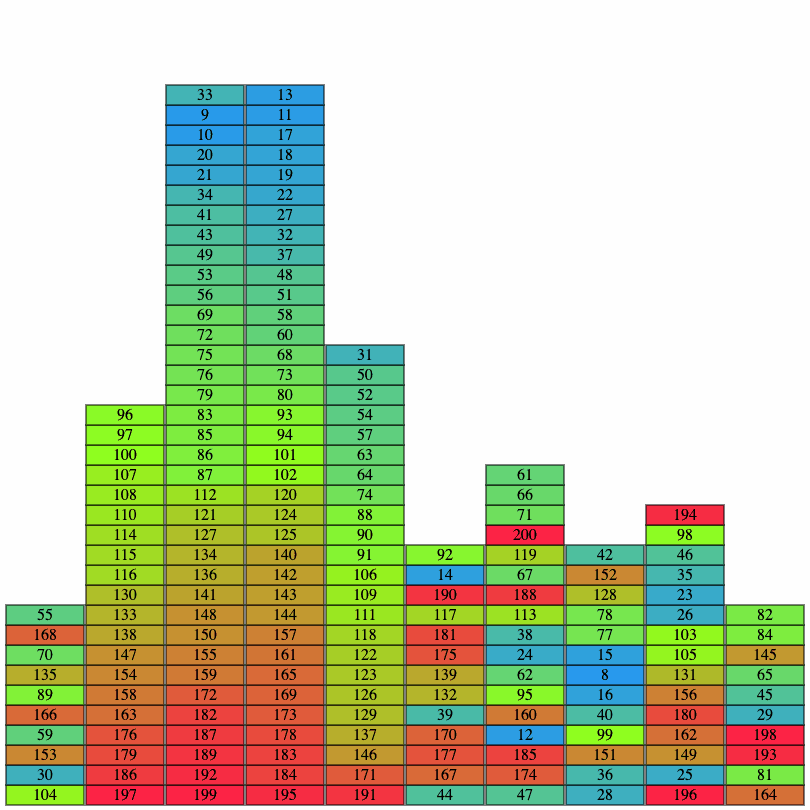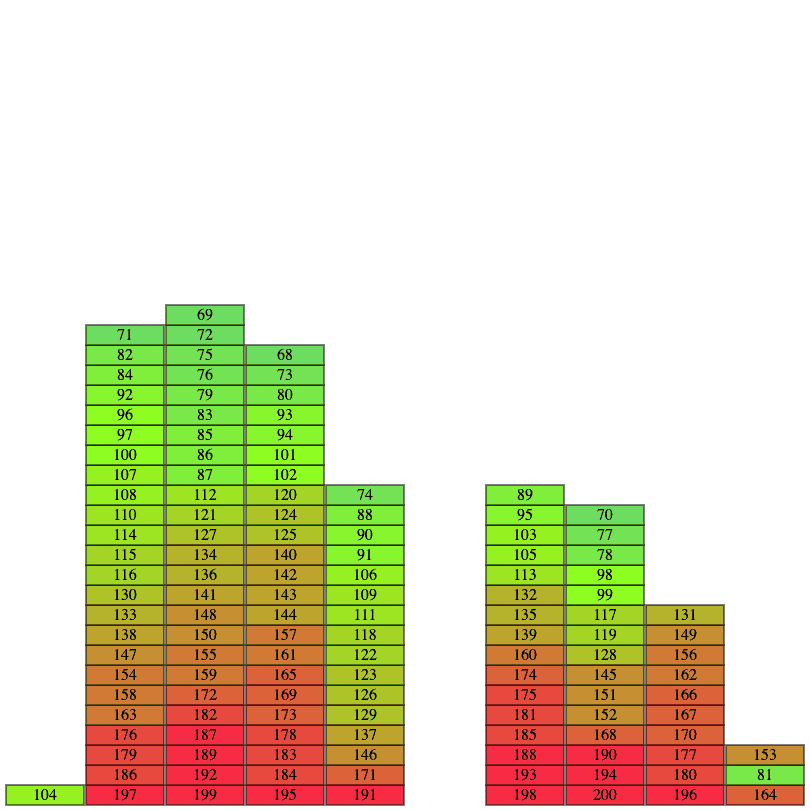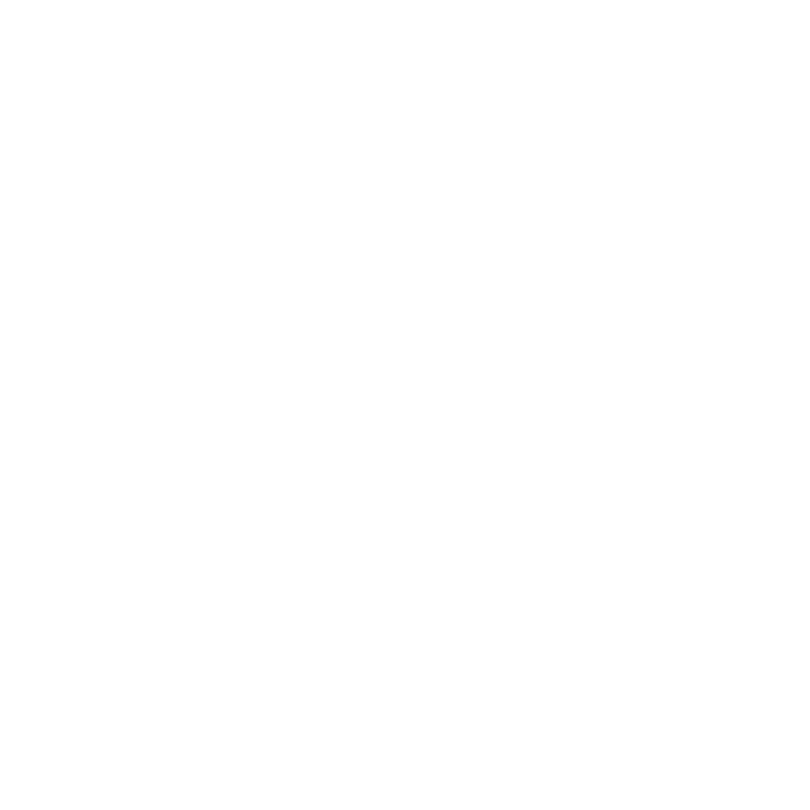
ビームサーチによる初期解生成
最初にビームサーチによる初期解の作成を行います。全てのマスを通りかつ初期位置に戻る経路を 1度の探索で求めるのは難しいので複数回に分けて探索を行いました。
具体的には以下のパートで構成されています
- 通常探索
- 未到達領域を埋める処理
- 初期位置に戻る経路探索
具体的には通常探索を複数回行った後に未到達領域を埋める処理を行って最後に初期位置に戻る経路を追加する感じになります。

通常探索
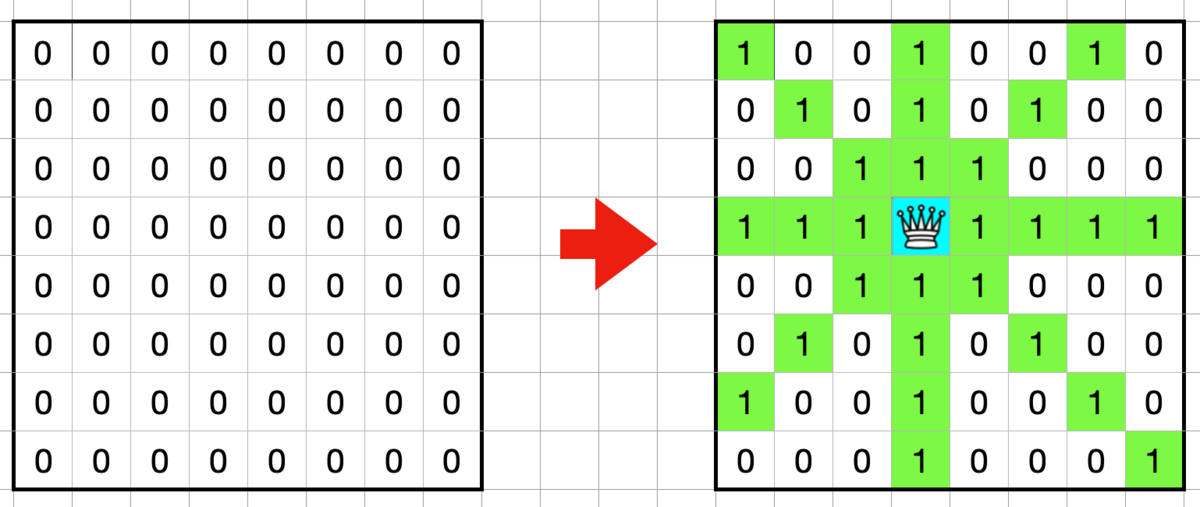
通常探索ではスコアを保ちつつ未到達領域の数を減らすような経路を探索します。スコアを評価関数にすると汚れにくいマスを探索してくれないので 到達済みのセルの数 を基本的な評価値にしました。また未到達領域の d の値については底上げを行って探索が行われやすくするようにして到達後は元の値に戻します。(今回は未到達のセルの d の値を +25 しています)
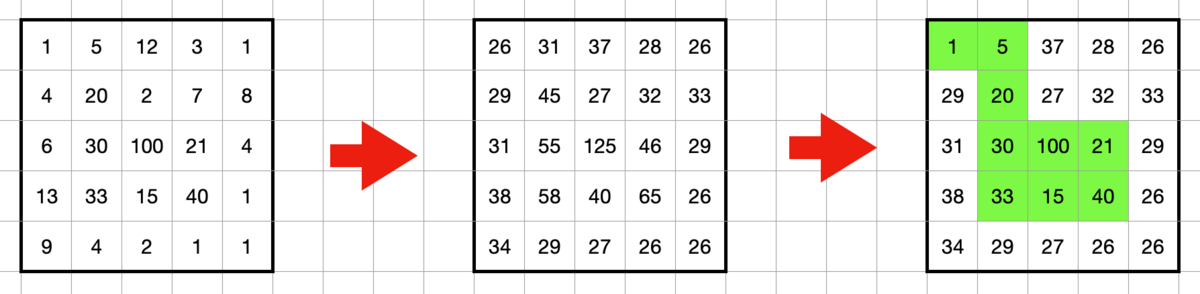
通常探索では 1回の探索で数百程度の長さの経路を作成して、未到達領域のセルの数が一定の数になるまでは経路探索を続けます。
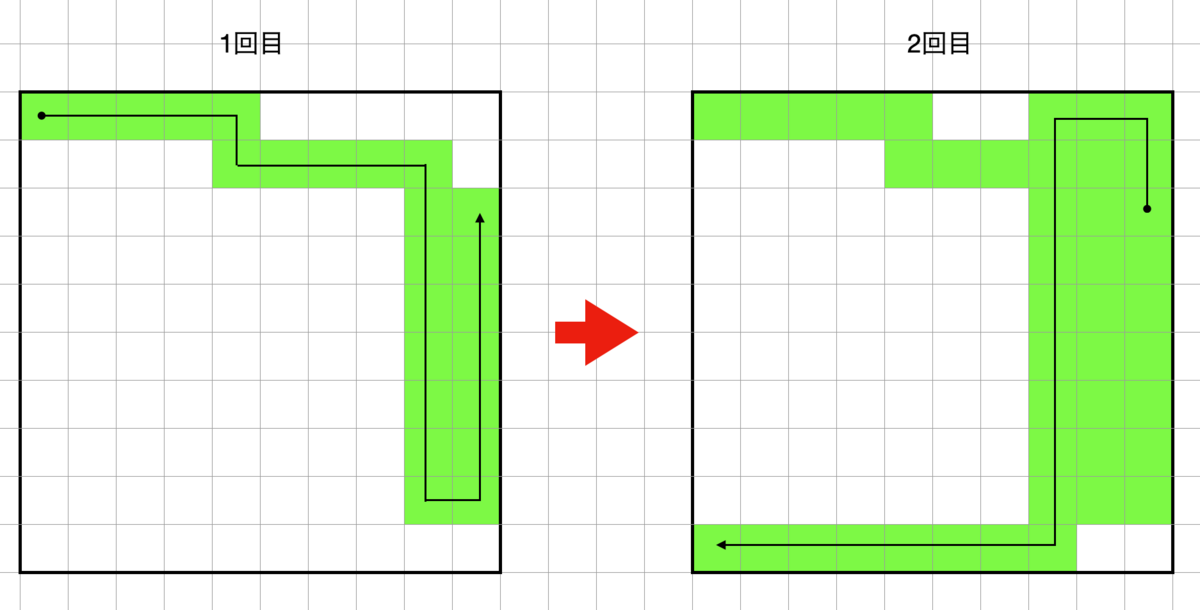
評価項目
通常探索における主な評価項目は以下の通りです
一度探索したセルをなるべく探索しないようにする
行って戻ってだったり、一度探索した箇所に再度訪れるみたいな行動は禁止しています。ただ行き止まりの通路から戻るときや周りに壁がある場合はその限りではありません。
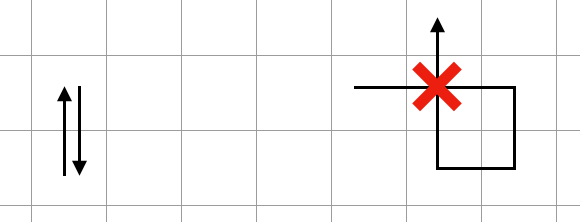
残りの未到達領域の数
通常探索で一番重要視している項目です。初期解パートではなるべく短い経路にしたいのでこの数が最終的な経路長にかなり直接的に関わってきます。ただし、経路長を重要視してしまうとスコアが悪化するのでそのあたりのバランスを取る必要があります。
生スコア
現時点で存在している汚れの総和と今までの汚れの総和の 2つを評価しています。残りの未到達領域の数 よりは低めに評価しています。
未到達領域を埋める
複数回通常探索を行うと図のようなほとんど探索したけどいくつか未到達領域が残っている状態になります。
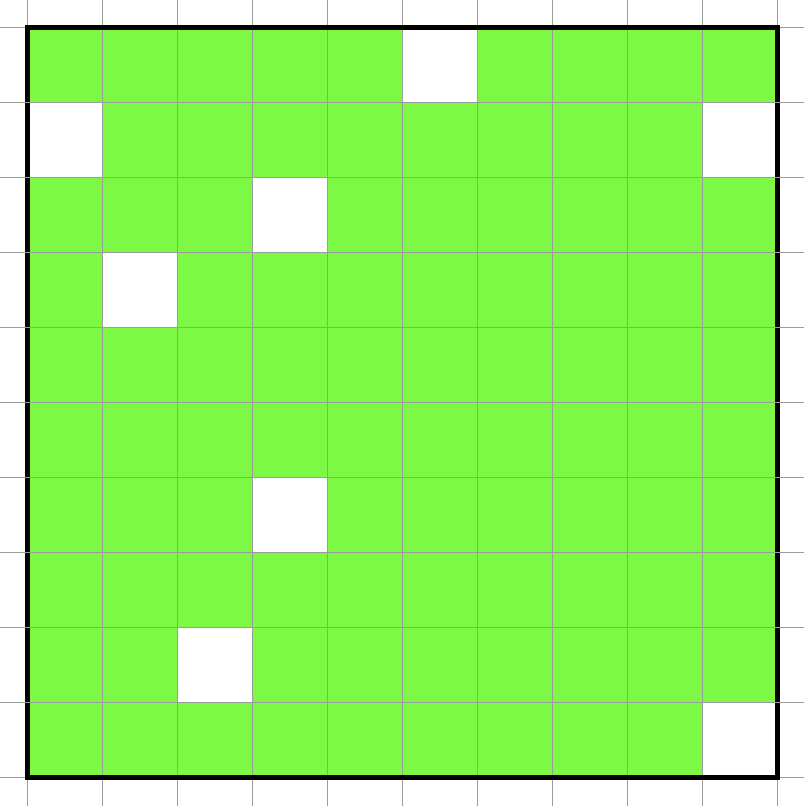
この状態から通常探索だけで全ての未到達領域を埋めようとするとかなりの経路長が必要になってしまうので別の方法で未到達領域を埋めていきます。
未到達領域に隣接している到達済みのセルが存在している場合 到達済みのセル -> 未到達領域のセル -> 到達済みのセル の経路を追加することで未到達領域のセルを消すことが出来ます。(元の経路から枝が生えたような感じになるので自分は 枝パス と読んでました)
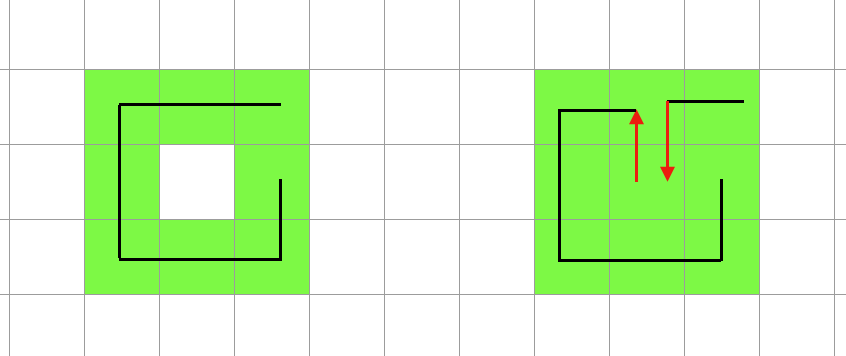
この処理を未到達領域がなくなるまで繰り返します。この処理のメリットとしては全体的なスコアをあまり落とさず未到達領域を消せるというところです。
この後の焼きなましパートでスコア計算を差分ではなくフルで行っているので同じぐらいのスコアであればなるべく経路長を短くしたいためこのような処理を行っています。(経路長 10000, スコア 2000 と 経路長 5000, スコア 2200 なら後者のほうが望ましい)
ビームサーチパートより焼きなましパートのほうが圧倒的にスコアが改善されるのでその試行回数を稼ぐ意味でもなるべく経路長は短くしたいです。
初期位置に戻る
全ての領域の探索が終わったら初期位置に戻る経路を作成します。特にこれといった処理は無いですが最短距離でなるべくスコアが良くなるような経路を探索しています。
初期解を複数作成して一番良いものを選ぶ
N が小さく時間に余裕があるケースについては複数回初期解を作成してその中で一番スコアが良いものを選びます。
焼きなましパートでは経路の一部を削除 & 作り直しを繰り返していきます。
経路の作り直し
経路の一部からランダムな長さ (2 ~ 8) を削除して再度経路を作り直します。
作り直す経路についてはものすごい小さなビーム幅のビームサーチで探索を行います。(今回だとビーム幅 3)
経路の制約
作り直す経路にはいくつか制約を設けています。
最大経路長
作り直す際の最大の経路長として 削除した経路の長さ + [2, 4, 6] から選ばれたランダムな値 を設定します。全部偶数なのは偶奇性の特徴から奇数を設定しても意味ないからです。この長さを超えるような経路を作成しようとした場合はその時点で切られます。
同じマスをなるべく踏まないようにする
ここは通常探索と同じく「行って戻って」だったり「ぐるぐる回って同じマスを踏む」のような行動を禁止しています。
削除した経路と同じ経路を作成しない
削除前と状態が変わらないので拒否します。
短い間隔でマスを踏まないようにする
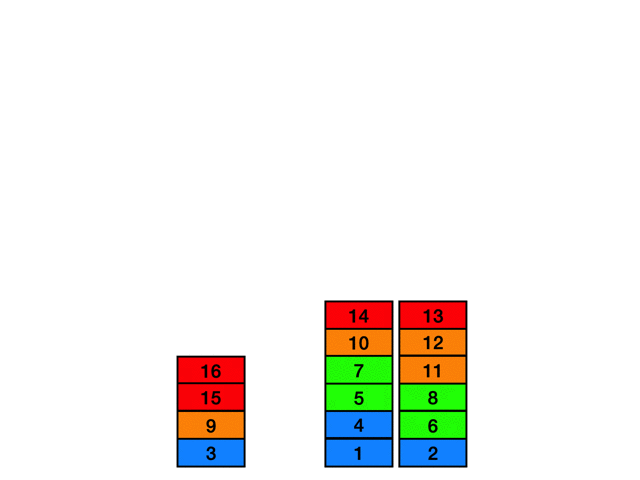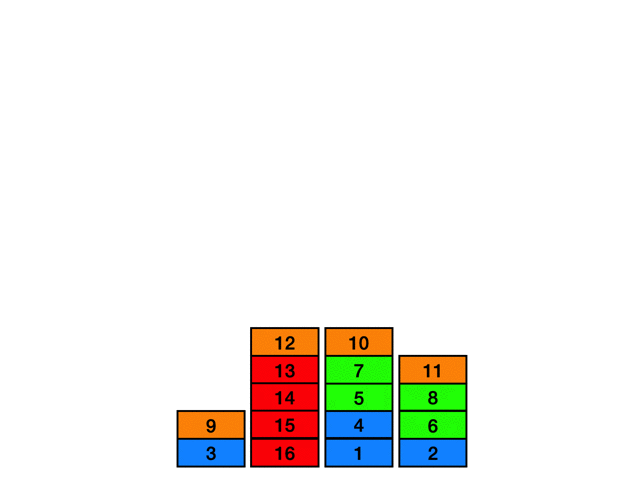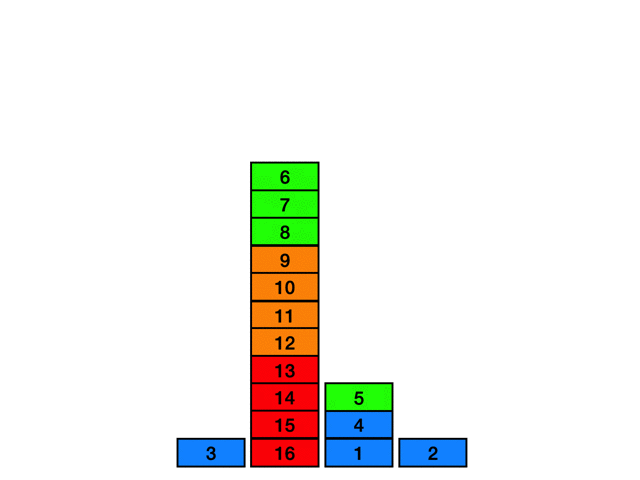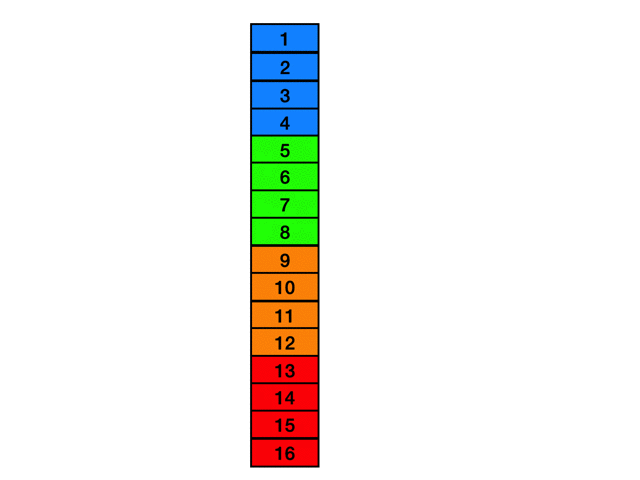
図のような時刻 7 - 10 時点の経路を削除して時刻 6 の位置から時刻 11の位置への経路を探索することを考えます。
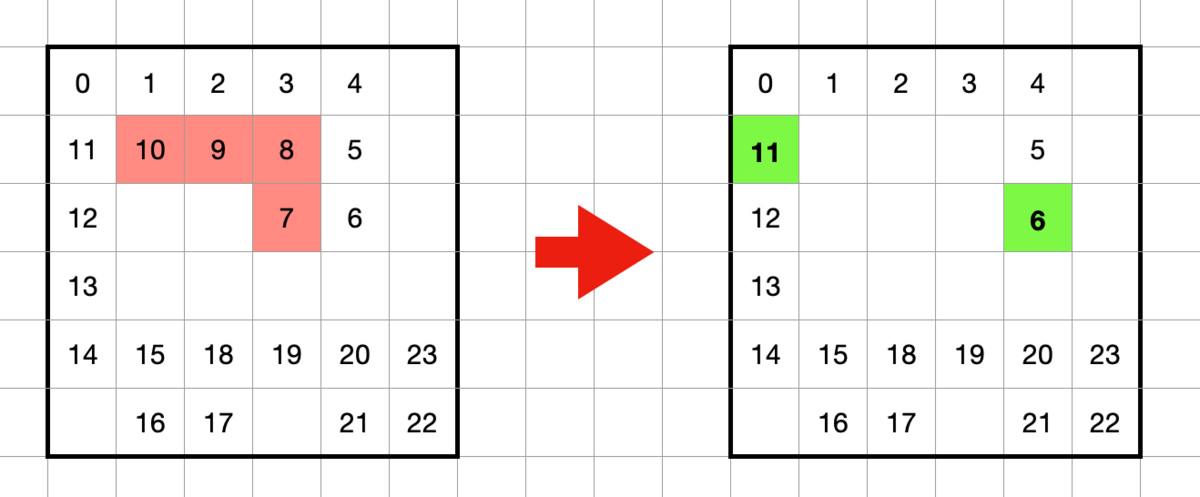
例として以下の図のように探索中に時刻 19の時点のマスに到達したとします。このときの間隔は 19 - 9 = 10 となり、この時間間隔が短すぎる場合はその経路を切り捨てます。
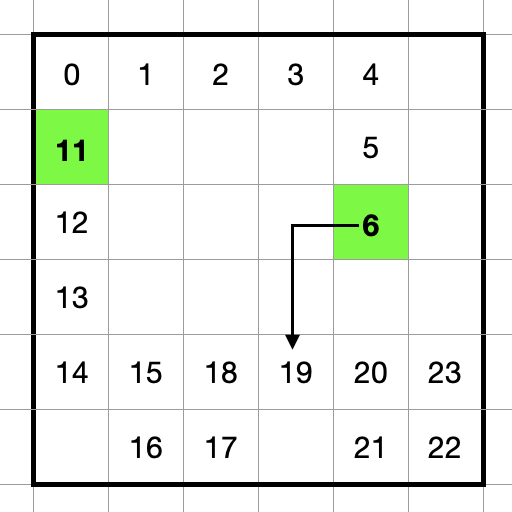
このようにすることで作り直した経路のスコアが悪化しにくくなるようにしています。
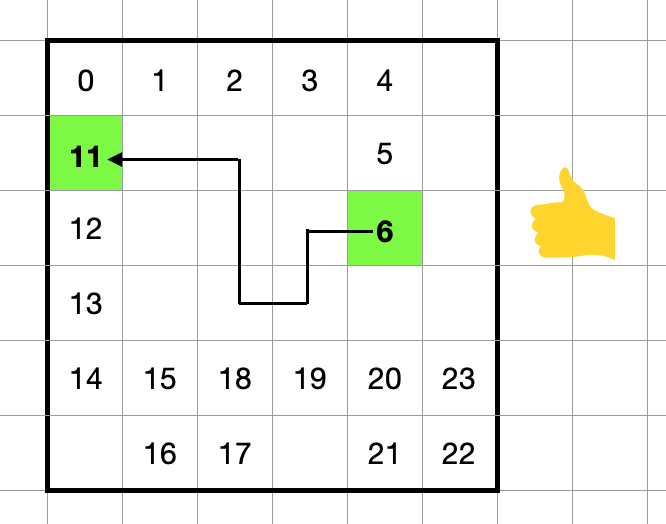
全てのセルの到達状態を維持する
経路を削除した際に未到達のセルが発生した場合はそのセルを通過しない経路を無効としています。
評価項目
作り直す経路の評価としては以下のようになります。
高速化のために評価はシンプルにしていて、これだけだと毎回似たような経路が作られるので乱数で適当な値を追加しています。
制約を緩めて再実行
上記の制約で新たな経路が見つからなかった場合(壁の影響で経路が作れないときがある)、制約を緩めて再度実行を行います。この際には重複マス排除やマスの到達間隔のチェックなどは行われません。
評価
作り直した結果を計算して評価します。スコアは生スコアそのままを使用しています。
感想
初期解作成 -> 焼きなましで改善というパターンで初期解の作成がかなり難しい問題。枝パスの存在を見つけてからは初期解作成の時間を短く出来たので焼きなましパートの時間を増やすことが出来たけど、スコアの差分計算が出来なくてこの部分にかなりの時間を取られてしまった。1位とはかなり点差があるので何か見落としているのは確実だけど結局最後までわからないまま。ヒューコンの最終日に何も出来なのは本当に良くないんだけど何が悪いと言われたら自分が悪いとしか言えないので精進するしかない。

お掃除ロボット高橋くん