Marathon Match 130 GraphLabeling Strategy

Problem

www.topcoder.com

Note

This article has been translated by DeepL. Original ver is here.

https://simanman.hatenablog.com/entry/2021/11/03/121958

Strategy

The general strategy is to determine the maximum value for labeling before, and then gradually reduce the maximum value if the entire node was successfully labeled, in a binary search-like strategy.

• Pre-determine the maximum value of label X to be given before labeling.
• Start labeling from a random point and visit each node recursively
• When labeling at each vertex, check if nodes with an even distance from the starting point can be labeled from 0 (0, 1, 2, ..., X). Nodes with odd distances are checked to see if they can be labeled from X (X, X - 1, X - 2, ..., 0).
• If labeling succeeds for all nodes, update the maximum X value (X = X / 2); if it fails, set a value slightly lower than the previous best value (X = BEST_X * random_value [0.95, 1.0))
• Repeat this procedure until the time limit is reached.

Determine the maximum value X of the label

Determine the maximum value when labeling is done. This way you will get a graph with a definite X score when the labeling is complete.

Labeling

Start from a random point and label it. Nodes with an even distance from the starting point will search for labels assignable from 0, and nodes with an odd distance will search for labels assignable from X.

Example for X = 100

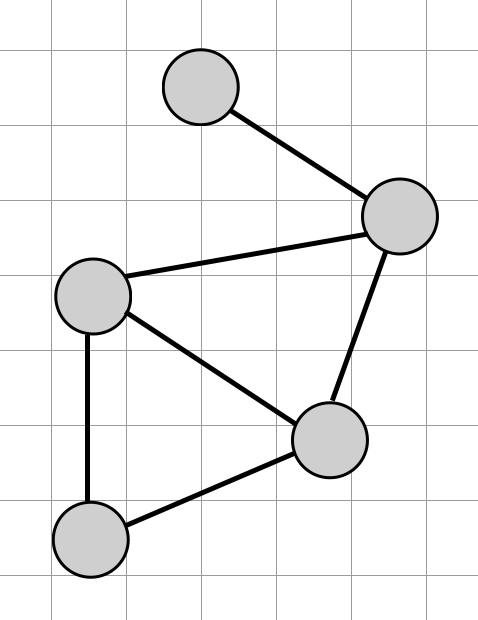
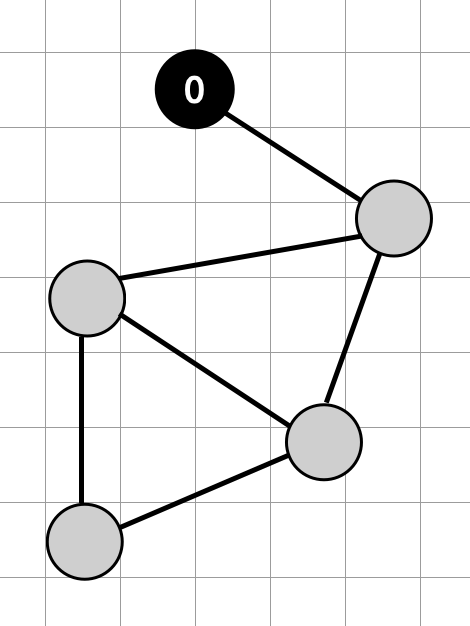
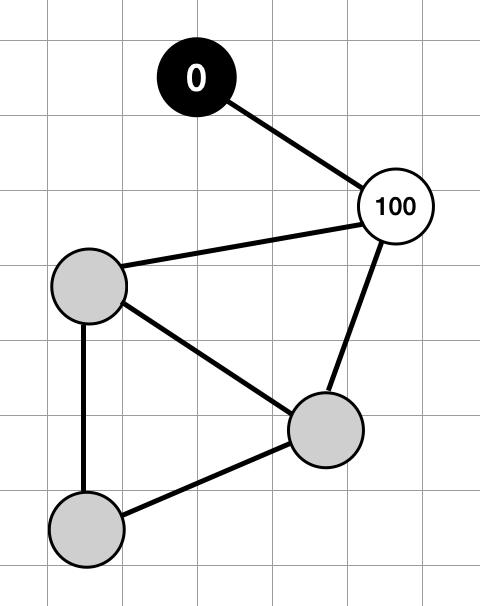
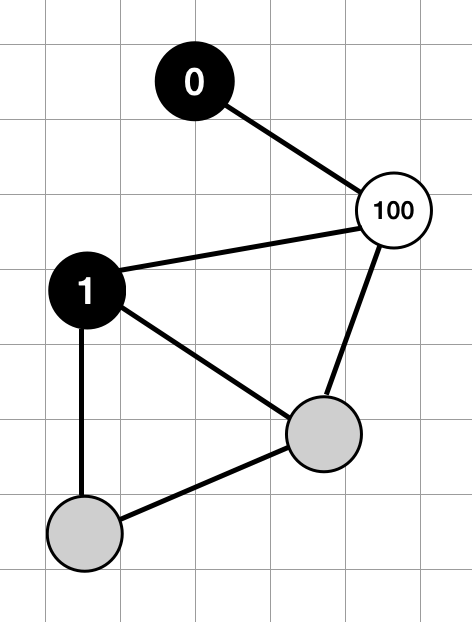
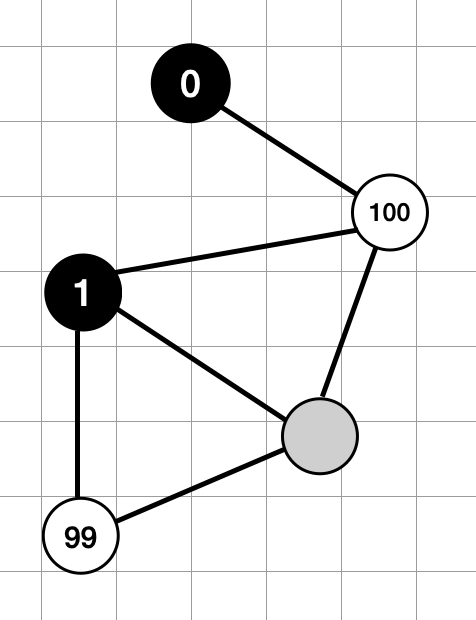
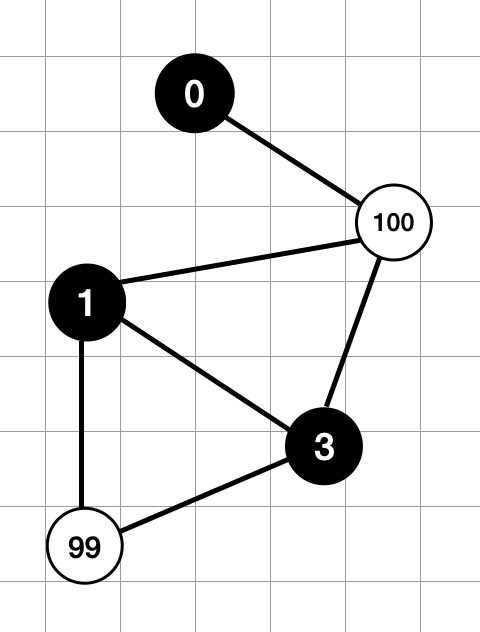
Since the labeling was successful for X = 100, we will do the same for the next attempt with the value of X = 50. If it fails, we randomly choose a value from the range X = [95, 99]. If it succeeds, it will lower the maximum value by a large amount, and if it fails, it will lower it by a small amount.

Repeat this process until the time limit and output the best labeling.

Summary

My overall score was low because I didn't know about the Gorom ruler, but I was able to get a high score on a sparse graph, so I put together a strategy.