It was a matter of efficiently dropping the blocks into the holes.
https://www.topcoder.com/challenges/82eb883d-85e9-442f-b0eb-91631d3d2a8f
方針
First, create an operation array in the order of dropping the base block.
There are several steps involved in creating an operation array.
Improving efficiency of 1-move drop
The first step is to list the blocks that can be dropped in one move, and find the order in which they are dropped by SA.
Since the operation of moving a block affects the operations before and after it, when the order of operations is changed, it is necessary to check each time whether the current operations is valid or not, and this cost is so large that it is difficult to do it.
However, if the order of the moves is reduced to [position of the hole, direction of block acquisition], there is no dependency between the previous and next move, so there is no need to check the feasibility of the move.
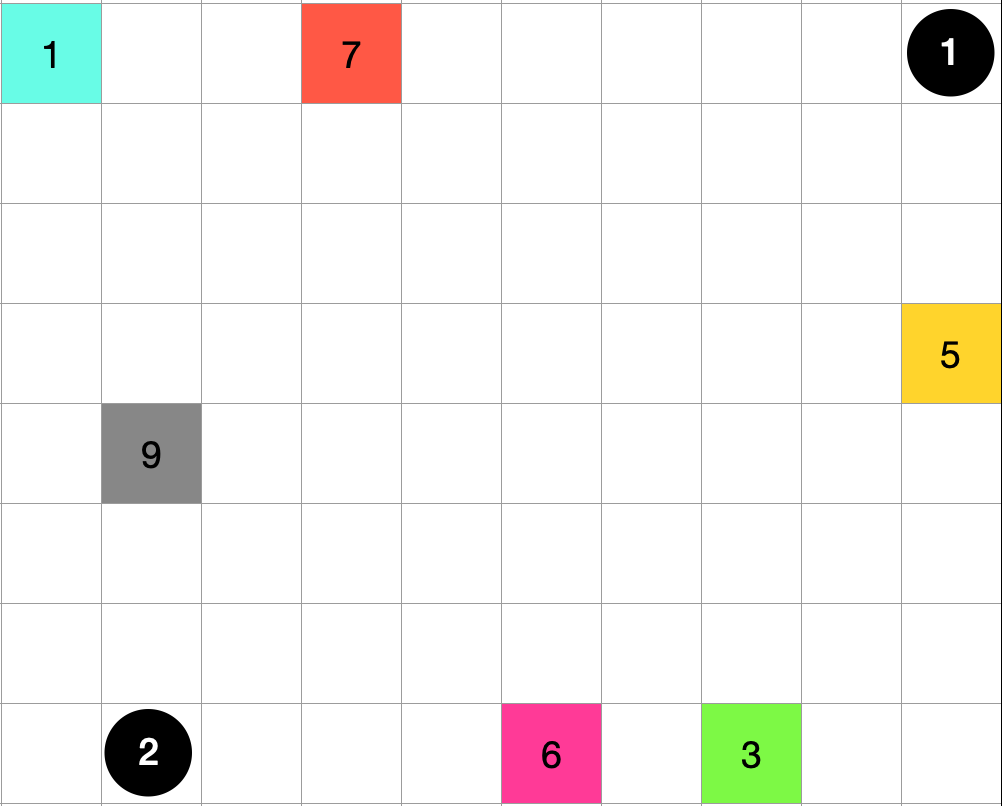
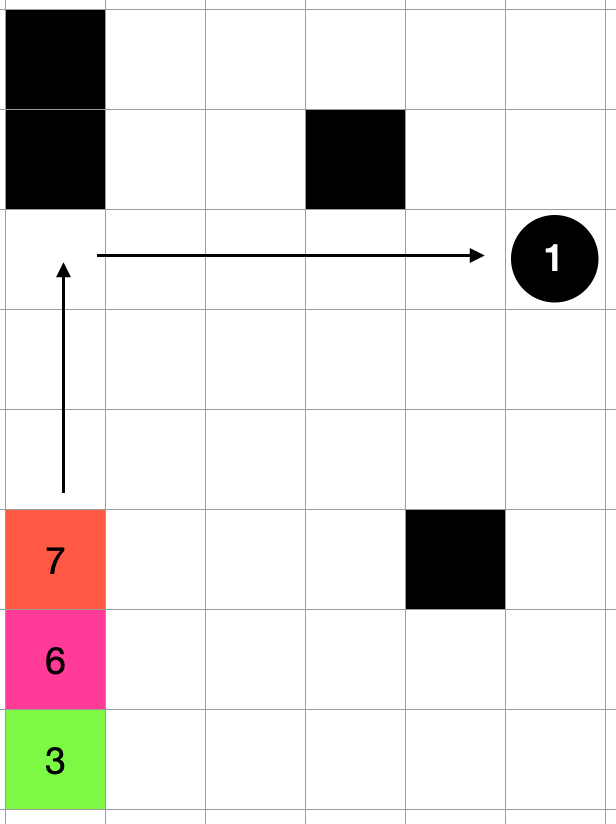
For example, if you are in the state shown in the image above
[[Hole 1, LEFT], [Hole 1, LEFT], [Hole 2, UP], [Hole 2, RIGHT], [Hole 1, DOWN], [Hole 2, RIGHT]]
It's like creating a sequence of operations like If you limit yourself to at least one move drop, this will give you a nearly optimal procedure.
However, when I dropped the 1 value block, I shifted it to the side instead of dropping it if it looked good, because shifting it to the side might increase the number of blocks for 2-move operations.
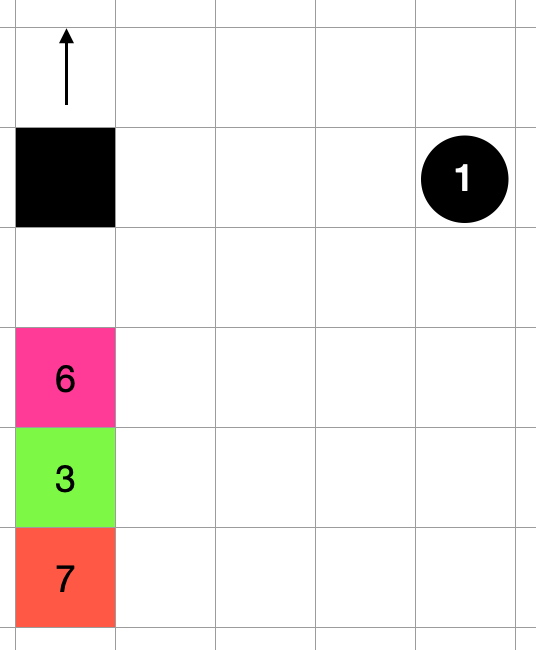
Greedily select operations.
Although 1-move operations are given priority, there are cases where the latter is actually more efficient than "1-move operations twice to drop blocks 2 and 3", such as "2-move operations to drop block 9". For this reason, we chose the one that seemed best while also running the process of greedily deciding the operation in parallel.
It greedily chooses an operation, but if the best operation is more than three moves, it runs a search to see if it can manipulate the board so that it becomes a two-move operation.
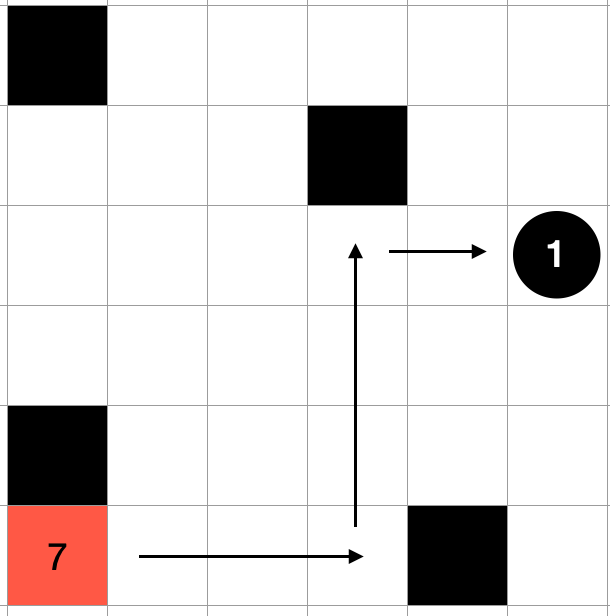
For example, in this situation, it would take three moves to drop the 7 block, but by sliding the block one move upper, it can be dropped in two moves.
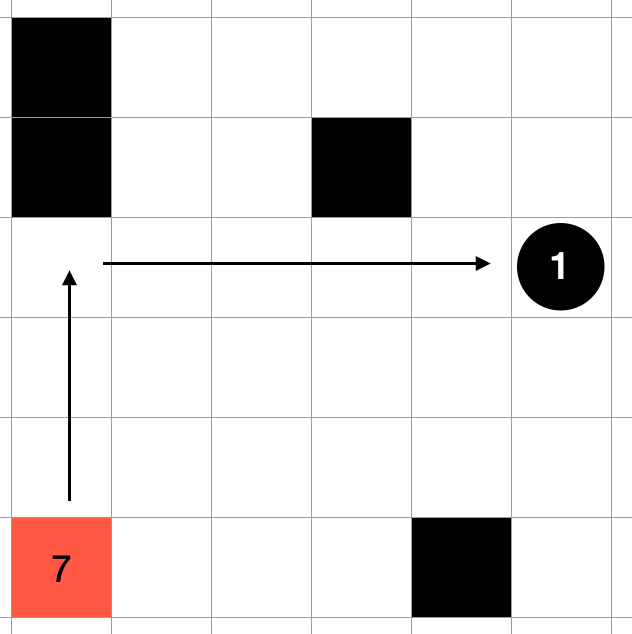
If you only look at this move, the result is the same: "drop the block of 7 in 3 moves" in both cases, but now that you can drop the block in 2 moves, the efficiency of dropping other blocks will also increase, resulting in a higher score.
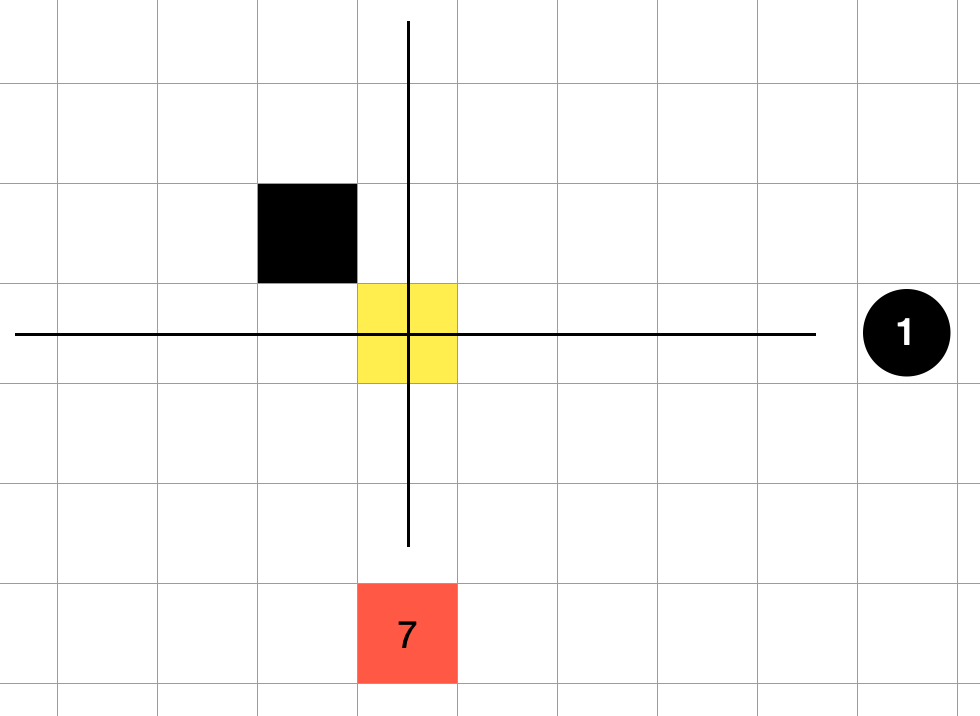
To check for the existence of such a board manipulation move, we check the orthogonal lines of "hole" and "block" and see if we can place a block in one square around the point.
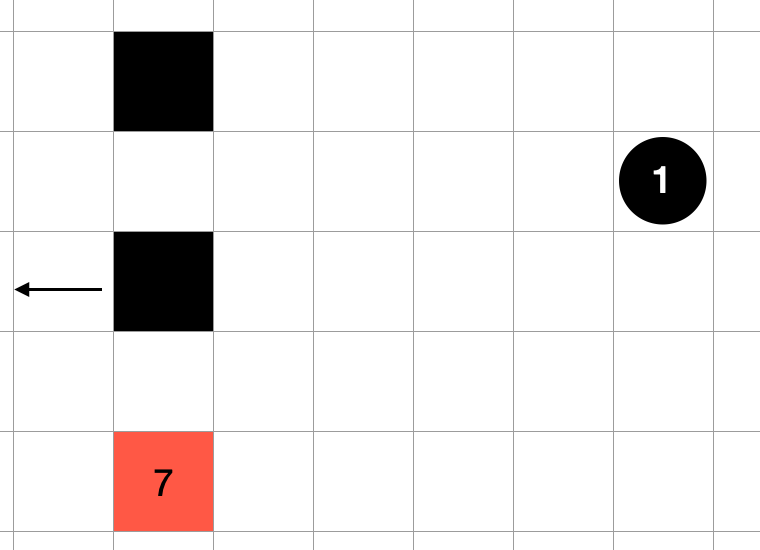
We have also included a process to remove the block of 1 to prevent "the block of 1 is blocking the 2-move operation".
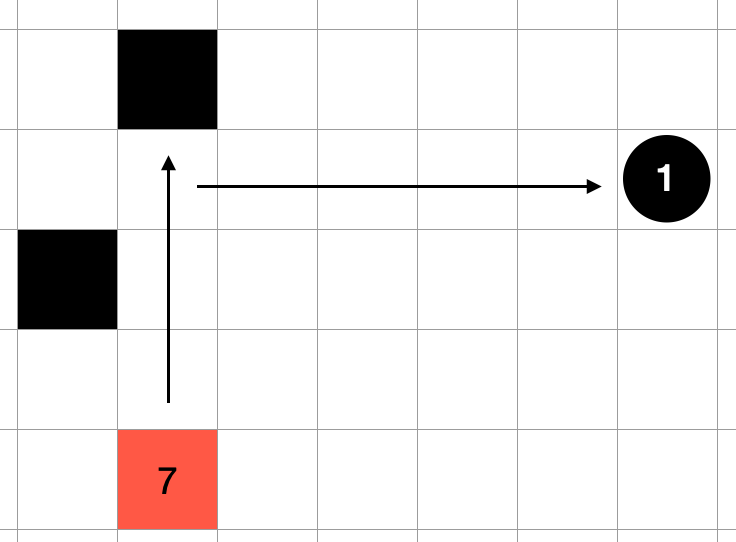
Calculate the expected value of the value by getting the block
For overall optimization, the score including several moves ahead is more important than the maximum value at that timing, so I roughly calculated the value and added it to the evaluation.
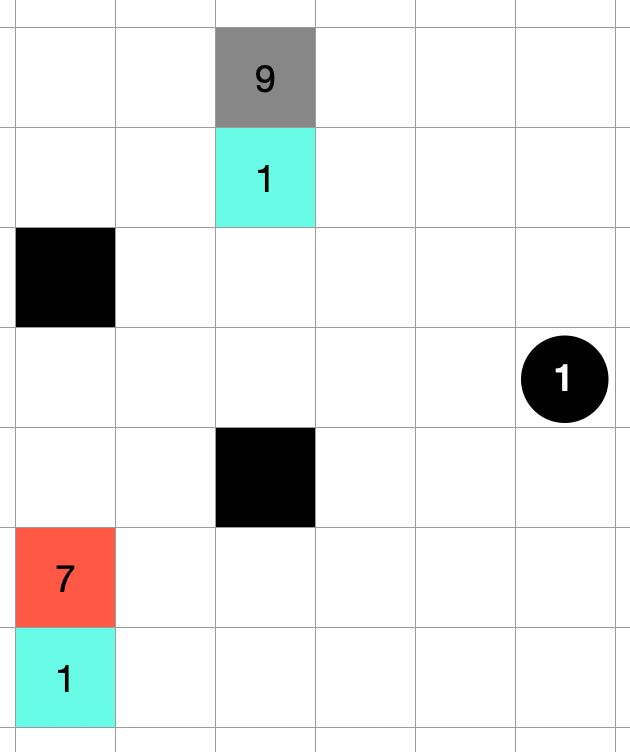
In the case of this image, processing it as [1, 9] would result in a higher score than processing it as [7, 1]. The evaluation was determined by the following code for the block that exists behind.
value += block_value / d d += random_value # random_value is randomly set to a value between [1.0, 3.0] that is randomly determined before the search.
I adopted it because it scored better than [sum of blocks] / [number of moves required], but I honestly don't know why.
Treat operations as events.
The final sequence of operations will be handled as an array of events, with "drop the block into the hole" as the delimiter. So
1 2 S R 4 6 S U 8 6 S U 6 5 M R 6 6 S U 0 2 M D
Instead of a flat operation array like
[
[1 2 S R],
[4 6 S U],
[
8 6 S U,
6 5 M R,
6 6 S U,
0 2 M D
]
]
It's like having an array of operations grouped in units of "drop blocks".

Change the order of operation of events.
Move and manipulate the array of events obtained at the end as long as the overall operation is not broken. If the move raises the overall score, the replacement is adopted. (Hill Climbing)
The way to do this is to skip the application of the event to be replaced, and continue applying the event until the subsequent event fails, and then calculate the score of "if this event is inserted at this timing" each time and insert it at the timing with the highest value.
Try this both from the front and from the back, and if you can't update the score, you're done. (In the case of backward, it's like doing the reverse operation for each event from the board after all events have been applied.
This is the end of the process.
Event binding process
For certain events, the dependencies are so strong that they cannot be replaced properly, so we try to reduce the number of targets for the reordering process by grouping events to some extent.

For example, in the image, the operation of inserting blocks in the order [7, 6, 9] is almost immutable, so we combined these events as one event instead of three. By grouping the events together, the variation in score that occurs in one replacement process becomes larger, and the range of improvement becomes larger, resulting in a higher score.
To determine whether or not to combine events, we used to judge whether or not the y-axis or x-axis of the coordinates of the first operation was equal. (If they are equal, the same decision is made.)
Repeat the process until the time limit is reached.
The rest of the process (procedure creation -> procedure replacement) will continue until the time limit is reached. Before execution, change the values of various parameters so that a different sequence of operations can be taken each time.
Impressions
I think the difference was in the greed to determine the operating procedure, and I realized once again that I lacked the ability to evaluate the board.